等离子体物理_pyk
麦克斯韦方程组
一般形式

对(2.2.2)两边求散度(左乘拉普拉斯算子),再联立(2.2.3)就可以推出电荷守恒方程(2.2.5)
洛伦兹力定律
F = q(E+v x B)
v是粒子速度
B= u0 ·H 是磁感应强度矢量
玻尔兹曼方程
引入一个六位相空间(r,v)中的分布函数f(r,v,t),r代表位置,t代表速度。
可以得到无碰撞玻尔兹曼方程,或弗拉索夫(Vlasov)方程
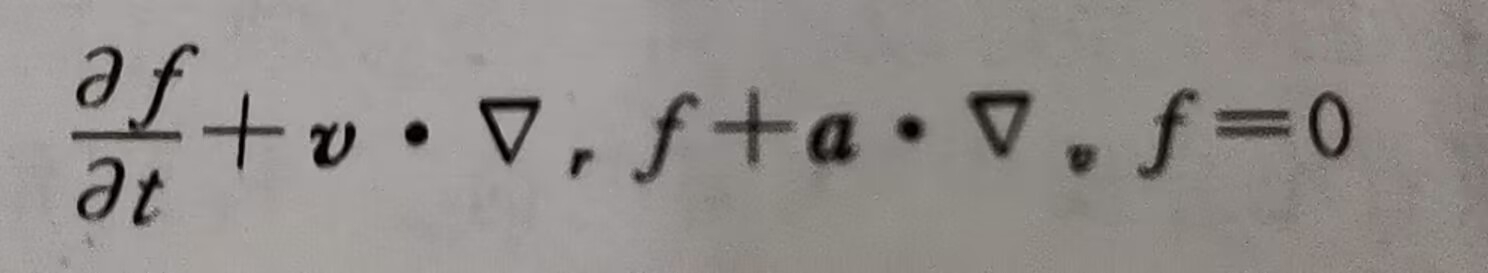
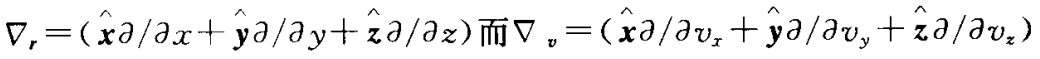
对其两边加上碰撞项,就得到玻尔兹曼方程
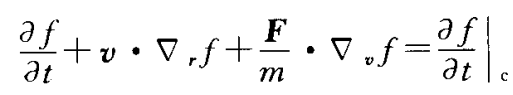
宏观量
粒子密度
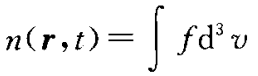
粒子通量
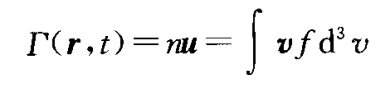
单位体积内粒子的动能
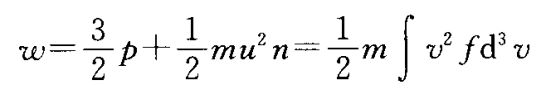
动量守恒方程&能量守恒方程
对玻尔兹曼方程两端成v,然后对速度积分,就是动量守恒方程
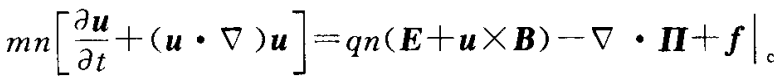
其常见表达式为
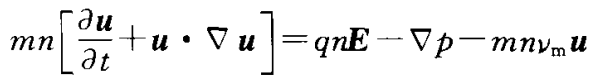
对玻尔兹曼方程两端同乘1/2mv^2,并对速度积分,能得到能量守恒方程
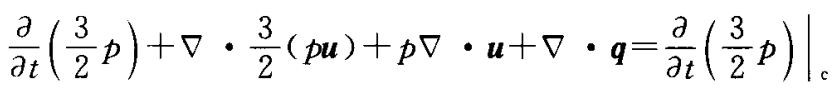
麦克斯韦分布
在没有空间梯度和加速度项的稳态情况下,玻尔兹曼方程简化为
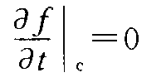
c代表同种粒子之间的碰撞,其解为一个有高斯形式的速度分布函数f(v)
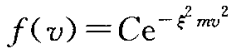
最终可以解出C和ξ可以得到
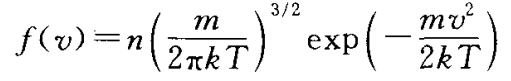
等离子体在均匀场中的运动
回旋频率
回旋半径
ExB漂移
电磁波
静电波
介电张量
波的色散关系
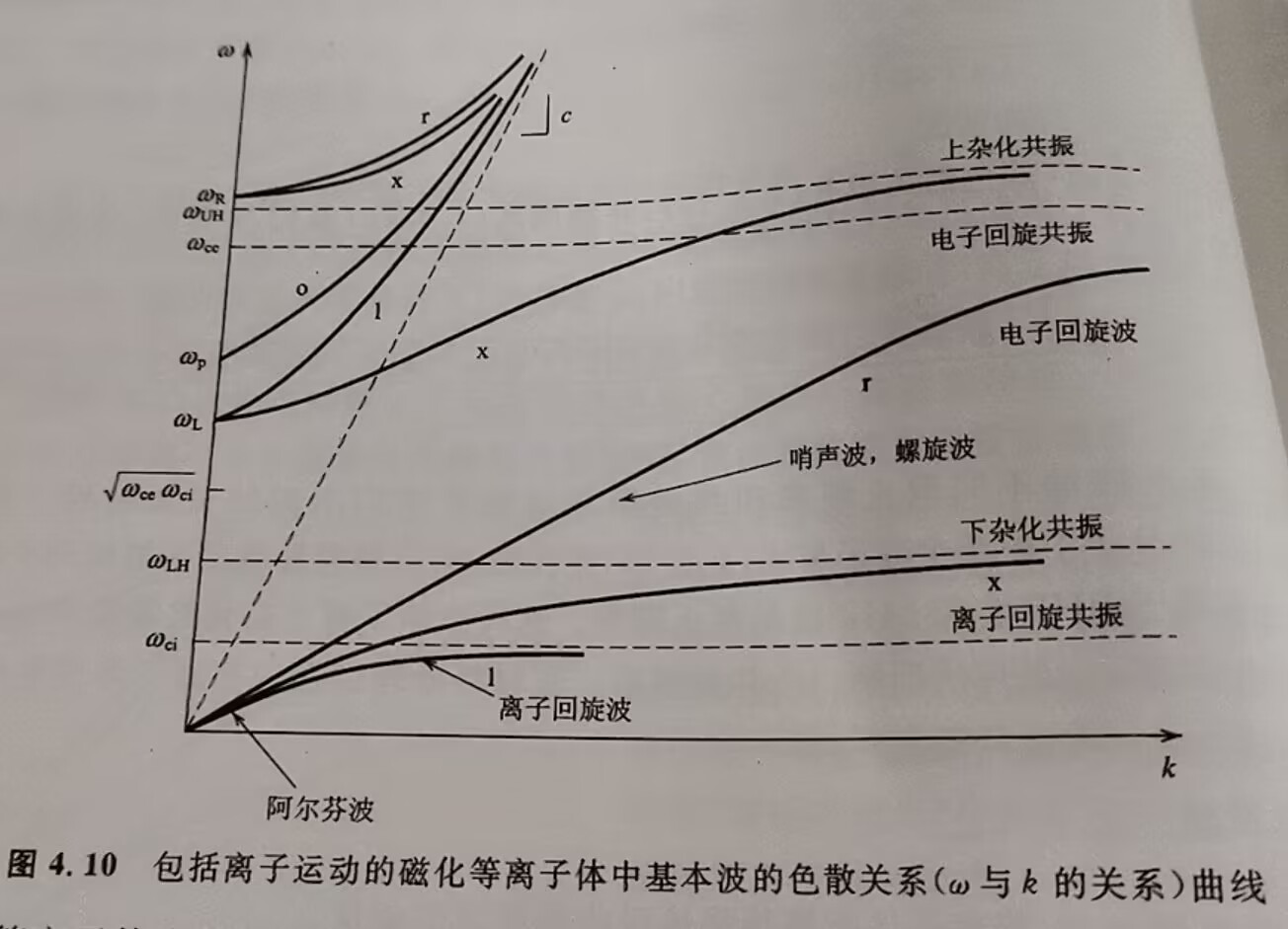
磁化等离子体中的波
IV曲线
chatGPT
我们可以利用IV曲线上的斜率来计算等离子体密度。在低压下,当电流随电压增加呈指数增长时,IV曲线上的斜率与等离子体密度成正比。因此,我们可以使用以下公式来计算等离子体密度:
n_e = (I_s/2πrLqA) * [(dV/dI) / V_p]
其中,n_e 表示等离子体密度;I_s 表示饱和电流;r 是探针半径;L 是探针长度;q 是电子电量;A 是探针截面积;dV/dI 是IV曲线的斜率;V_p 是等离子体的诱导电压。
需要注意的是,这种方法只能用于计算等离子体密度的数量级,而无法得到精确值。同时,由于该方法对实验条件要求较高,可能存在误差。
对于弱等离子体(即电离度较低),可以使用Langmuir剖面计算等离子体密度:
n_e = (I_sat / A) * ((4ε_0me)/(e^2π^2))^(1/2)
其中,n_e表示等离子体密度;I_sat表示探针饱和电流;A表示探针表面积;ε_0表示真空介电常数;m_e表示电子质量;e表示元电荷。
对于强等离子体(即电离度较高),可以使用Saha-Boltzmann方程计算电子密度:
n_e = (2πm_e k_B T_e/h^2)^(3/2) * (N_i/N)^2 * exp((-E_i/k_B T_e)* (1-β))
其中,N_i表示第i种粒子的数密度;N表示总数密度;T_e表示等离子体电子温度;k_B表示玻尔兹曼常数;h表示普朗克常数;E_i表示第i种粒子的电离势;β表示热化学平衡指数,通常在1左右。
Wang
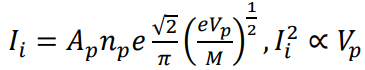
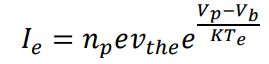

Vp是IV曲线的拐点
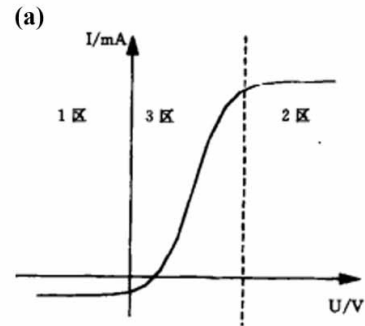
EEDF
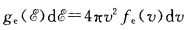
chatGPT方案--展开查看
等离子体的EEDF(能量电子分布函数)描述了等离子体中电子的能级分布情况,是等离子体物理学中一个重要的参数。以下是计算等离子体EEDF的基本步骤:
选取合适的实验方法来测量等离子体的电子能谱。常用的实验方法包括:光电子显微镜、辐射法、气体磁谱计等。
对于得到的电子能谱进行预处理,并将其转换为电子能量分布函数。通常,可以使用不同的数值技术和算法来进行预处理和转换。
根据转换后的电子能量分布函数,计算出等离子体的EEDF。这可以通过应用Boltzmann方程或其他相关方程进行计算。Boltzmann方程给出了EEDF的形式,可以写成下面的形式:
f(E) = A * exp(-E/kT_e)
其中,E是电子能量;T_e是电子温度;A是归一化常数。
对于复杂等离子体,例如非平衡等离子体,可能需要考虑更多的因素并采用更加复杂的模型来计算EEDF。在这种情况下,可以结合数值模拟和实验数据来进行计算和分析。
计算等离子体EEDF的公式通常基于Boltzmann方程,其形式如下:
f(E) = A * exp(-E/kT_e)
其中,f(E)是电子能量分布函数;E是电子能量;T_e是等离子体电子温度;A是归一化常数。
计算EEDF需要确定电子能量分布函数中的参数,包括归一化常数A和电子温度T_e。这可以通过将实验数据与理论模型进行比较来获得。
对于平衡态等离子体,可以使用以下公式计算电子密度n_e和电子温度T_e:
n_e = n_0 * exp(-E_i/kT_e)
T_e = (2/3)*(kT_n/m_e)
其中,n_0是等离子体中的中性原子或分子浓度;E_i是电离势;T_n是等离子体中的中性粒子温度;m_e是电子质量;k是玻尔兹曼常数。
归一化常数A是EEDF中的一个重要参数,它通常用于确保电子能量分布函数f(E)的总积分为1。确定归一化常数A的方法可能因实验条件和等离子体类型而异,但以下是一些常见的方法:
使用计算机模拟来估计归一化常数A。可以通过对Boltzmann方程进行数值求解来获得电子能量分布函数,并根据总积分为1的条件来确定归一化常数A。
使用实验数据来确定归一化常数A。这可以通过将实验得到的电子能谱与理论模型进行比较来实现。首先,需要计算出理论上的电子能谱,并使用已知的归一化常数A来匹配实验结果。然后,通过比较实验数据和模型预测值的差异来调整归一化常数A的值。
采用标准归一化常数。有时候,也可以使用标准归一化常数(例如,SI制中的1/m^3)来简化计算过程。这意味着电子能量分布函数f(E)将被除以总电子密度n_e,以确保总积分为1。
EEPF
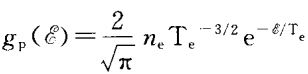
单粒子方程
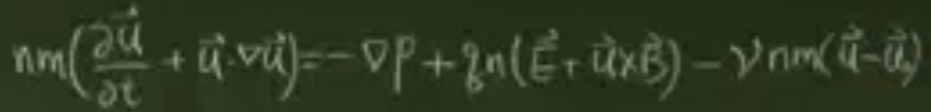
第一项是压力梯度项
第二项是qn洛伦兹力
第三项是碰撞项
离子束守恒(速率平衡方程)
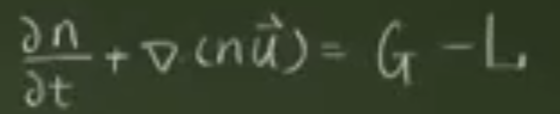
右边分别是产生项-损失项
对于1式中u比较小,所以可以省略,最终化简为以下式子
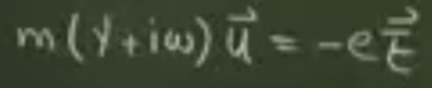
电子电流

u是平均速度
综上就可以推出欧姆定律(?)
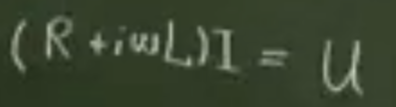
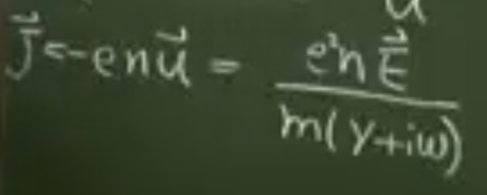
又知道j =电导率xE,所以根据上式就可以得出等离子体的电导率.
