色散关系

在物理科学和电气工程学中，色散关系描述波在介质中传播的色散现象的性质。色散关系将波的波长或波数与其频率建立了联系。由这组关系，波的相速度和群速度有了方便的确定介质中折射率的表达式。克拉莫-克若尼关系式可以描述波的传播、衰减的频率依赖性，这关系比与几何相关和与材料相关的色散关系更具一般性。

色散

当不同波长的平面波表现出不同的传播速度时，色散会发生，如此造成混合各种波长的波包渐渐地在空间中扩展开来。平面波的速率v为波长λ的函数：

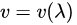
波速、波长、频率f之间具有恒等式：

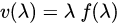
函数f(λ)指出了该介质中的色散关系。色散关系更常用角频率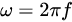与波数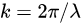来表示。上述式子可改写为

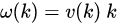
在此ω成为k的函数。使用ω(k)来描述色散关系已经成为一种标准写法，因为相速度 ω/k 与群速度 ∂ω/∂k 可以轻松地从这样写法的色散关系中求得。

因此所关注的平面波可写为如下数学式：

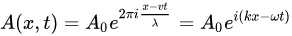
其中

A是波的振幅，

A0 = A(0,0)，

x是波传递方向上的任一特定位置，

t是描述波的任一特定时间。

对真空中的电磁波而言，角频率与波数呈正比：

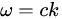
这是“线性”的色散关系。在此情形下，相速度与群速度乃是相同的：

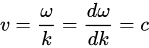
两者皆为c，真空中的光速，为与频率无关的常数。

粒子的总能量、动量与质量透过如下相对论关系连结：

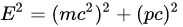
其中m是静质量。

当静质量m为零时，比如光子的例子：

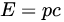
又静质量不为零的粒子，当其接近光速时，pc项远大于mc^2项，因此关系式可趋近于E = pc。其在非相对论极限，也就是速度远小于光速c的情形，可趋近于如下关系式：

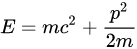
此情形下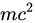，是常数，而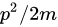是常见的动能，可以动量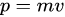来写出关系式。

从近光速的例子过渡到低速度极限，可看到E与p的关系是从p转成p^2，在垂直轴跟水平轴皆取对数log的色散关系图中可看出斜率的改变。

基本粒子、原子核、原子，甚至是分子，皆有物质波的波动表现。根据描述物质波的“德布罗意关系”，能量E与角频率ω之间以及动量p与波数k之间皆为正比关系，比值为约化普朗克常数ħ：

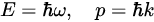
相应地，角频率与波数之间也可透过色散关系连结。在非相对论极限（低速度极限的牛顿力学）条件下，利用能量（动能）与动量的关系式：

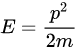
此处省去常数mc^2的效应。等式左右分别代入德布罗意关系，可得色散关系：